Incinerator Drone: Difference between revisions
HeadshotTAS (talk | contribs) No edit summary |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
==How the RNG Works== | ==How the RNG Works== | ||
[[File:IncineratorDrone.png|thumb|upright=2.0]] | |||
The round time | The first round time takes between 8 and 13 seconds (480-780 frames), and the remaining rounds take between 15 and 25 seconds (900-1500 frames). Since it is assumed that 1 frame passes between each of the rounds, the overall amount of time it takes is between 53.05 and 88.067 seconds (3183-5284 frames).<br><br> | ||
This is how the Random Number Generation works for this fight: | This is how the Random Number Generation works for this fight:<br><br> | ||
1. A random unsigned 16-bit integer (between 0 and 65535) is generated.<br> | |||
2. That number is divided by 65535, and the result is stored as a single-precision (32-bit) float. This number is always between 0 and 1.<br> | |||
3. A 32-bit floating point timer is initialized with an initial value of (5 * x) + 8 for the first round and (10 * x) + 15 for the rest, where x is the result from step 2.<br> | |||
4. Every frame, 1/60 is subtracted from the timer.<br> | |||
5. When the timer hits zero, the weak point becomes exposed.<br> | |||
6. The process is repeated until the I-Drone has no more hitpoints.<br> | |||
<br> | |||
There are 301 possible durations (numbers of frames) for the first round and 601 possible durations for the rest. Since there are 65536 possible random numbers, each duration for the first round should correspond to about 218 different random numbers, and each duration for the rest should correspond to about 109 different random numbers. | There are 301 possible durations (numbers of frames) for the first round and 601 possible durations for the rest. Since there are 65536 possible random numbers, each duration for the first round should correspond to about 218 different random numbers, and each duration for the rest should correspond to about 109 different random numbers. | ||
| Line 33: | Line 34: | ||
===Everything in between=== | ===Everything in between=== | ||
This [https://github.com/Skull64/metroid-rocks/tree/master/i_drone code] calculates the probability of I-Drone taking every possible number of frames. It also displays the cumulative probability of it taking all numbers of frames less than or greater than every possible number of frames. | This [https://github.com/Skull64/metroid-rocks/tree/master/i_drone code] calculates the probability of I-Drone taking every possible number of frames. It also displays the cumulative probability of it taking all numbers of frames less than or greater than every possible number of frames. | ||
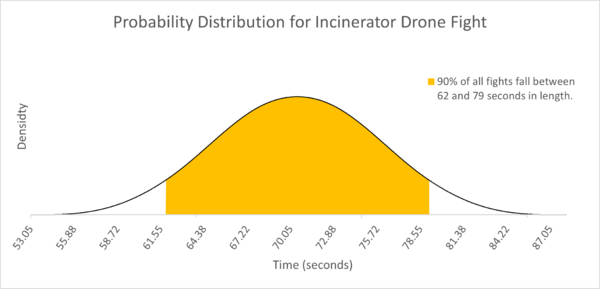
* 90% of all fights fall between 62 and 79 seconds in length. | |||
* Average fight length ~ 70.55 seconds standard deviation of ~ 10.1 seconds. | |||
* 1.96% of fights are 60 seconds or faster. | |||
* 3.41% of fights are 80 seconds or slower. | |||
One of the slowest I-Drone fights was timed to have taken 85.933 seconds (5156 frames) after subtracting the time it took to shoot the weak points after they became visible. The code calculated that the probability of I-Drone taking 5156 or more frames is 1/6064. Thus it could be said that only 1/6000 or so I-Drone fights could be expected to have worse RNG than the RNG in that fight. | |||
==See Also== | ==See Also== | ||
Latest revision as of 23:09, 20 October 2021
The Incinerator Drone (I-Drone) is a miniboss in the Burn Dome in Chozo Ruins. It guards the Morph Ball Bomb.
The Incinerator Drone must be damaged sufficiently 4 times before it is destroyed. It can only be damaged when its weak point is exposed. Where the weak point appears is not random. The weak spot is exposed either facing North to South or East to West room and alternates every other round starting with facing the East to West. There is a standable ledge around Incinerator Drone right in front of its top. In standing here, you can't get hit by the flames and can spawn kill the War Wasps. This lets you quickly shoot the weak spot, making the fight trivial. There are 4 rounds to the fight. The amount of time it takes to expose its weak point is random each time, but there are limits. After defeating Incinerator Drone you will fall into Morph Ball Bomb.
During the Fight
- Incinerator Drone is vulnerable to Ice Beam, which can be obtained before the fight using Out of Bounds. (see also: Early Ice Beam)
- The Morph Ball tunnel blockage is damageable with Power Bombs which can be obtained before the fight using Out of Bounds. This allows you to get the Missile Expansion in this room during the fight. (see also: Power Bombs Before Bombs)
How the RNG Works
The first round time takes between 8 and 13 seconds (480-780 frames), and the remaining rounds take between 15 and 25 seconds (900-1500 frames). Since it is assumed that 1 frame passes between each of the rounds, the overall amount of time it takes is between 53.05 and 88.067 seconds (3183-5284 frames).
This is how the Random Number Generation works for this fight:
1. A random unsigned 16-bit integer (between 0 and 65535) is generated.
2. That number is divided by 65535, and the result is stored as a single-precision (32-bit) float. This number is always between 0 and 1.
3. A 32-bit floating point timer is initialized with an initial value of (5 * x) + 8 for the first round and (10 * x) + 15 for the rest, where x is the result from step 2.
4. Every frame, 1/60 is subtracted from the timer.
5. When the timer hits zero, the weak point becomes exposed.
6. The process is repeated until the I-Drone has no more hitpoints.
There are 301 possible durations (numbers of frames) for the first round and 601 possible durations for the rest. Since there are 65536 possible random numbers, each duration for the first round should correspond to about 218 different random numbers, and each duration for the rest should correspond to about 109 different random numbers.
Best possible RNG
For the rounds other than the first, the there are 109 initial random numbers (0-65535) that result in the minimum number of frames (900), which are 0-128. For the first round, however, it turns out that there is only 1 initial random number that results in the minimum number of frames (480), which is 0. This is due to the nature of floating-point arithmetic. The probability of getting a perfect round is thus 1/65536 for the first round and 109/65536 for the other three rounds, for an overall probability of (1)*(109)^3 / (65536)^4, or (109^3) / (2^64), or about 7.02e-14, or about 1 in 14 billion.
Worst possible RNG
For the rounds other than the first, there are only 2 initial random numbers (0-65535) that result in the maximum number of frames (1500), which are 65534-65535. For the first round, there is again only 1 initial random number that results in the maximum number of frames (780), which is 65535. The probability of getting the worst possible round is thus 1/65536 for the first round and 2/65536 for the other three rounds, for an overall probability of (1)*(2)^3 / (65536)^4, or 1 / (2^61), or about 4.34e-19, or about 1 in 2.3 quintillion.
Everything in between
This code calculates the probability of I-Drone taking every possible number of frames. It also displays the cumulative probability of it taking all numbers of frames less than or greater than every possible number of frames.
- 90% of all fights fall between 62 and 79 seconds in length.
- Average fight length ~ 70.55 seconds standard deviation of ~ 10.1 seconds.
- 1.96% of fights are 60 seconds or faster.
- 3.41% of fights are 80 seconds or slower.
One of the slowest I-Drone fights was timed to have taken 85.933 seconds (5156 frames) after subtracting the time it took to shoot the weak points after they became visible. The code calculated that the probability of I-Drone taking 5156 or more frames is 1/6064. Thus it could be said that only 1/6000 or so I-Drone fights could be expected to have worse RNG than the RNG in that fight.